USEFUL FORMULAS
(Three Phase)
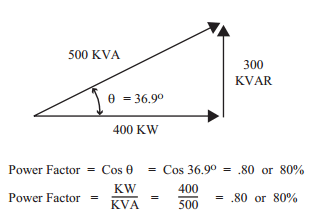
POWER FACTOR
and the
POWER TRIANGLE
| VOLTAGE CONSTANTS | ||
|---|---|---|
| For 208 Volts | 61.31 MFD / KVAR | 2.78 Amps / KVAR |
| For 240 Volts | 46.05 MFD / KVAR | 2.41 Amps / KVAR |
| For 480 Volts | 11.51 MFD / KVAR | 1.20 Amps / KVAR |
| For 600 Volts | 7.37 MFD / KVAR | 0.96 Amps / KVAR |
Power Losses due to the transmission of current can be significantly lowered with the improvement of Power Factor. This benefit is mainly realized where there are long conductor runs to motors or electrical distribution systems are heavily loaded. Known as I2R losses, the formula for calculating the reduction of these losses is shown as follows:
$$( \hspace{3 pt}Loss \hspace{3 pt}Reduction \hspace{3 pt}= 100 – 100 \hspace{3 pt}* \begin{pmatrix} \frac{Original \hspace{3 pt}PF}{Improved \hspace{3 pt}PF}\end{pmatrix}^{2})$$
Capacitors can increase the system voltage. This increase is beneficial in electrical systems where voltage drops are a problem. The calculation is shown as follows:
$$( \hspace{3 pt}Voltage \hspace{3 pt}Rise \hspace{3 pt}=frac{Capacitor \hspace{3 pt}KVAR \hspace{3 pt}x \hspace{3 pt} \hspace{3 pt} Transformer \hspace{3 pt} Reactance}{Transformer \hspace{3 pt}KVA} )$$
| Legend | |
|---|---|
| A | Amps |
| V | Volts |
| KV | Kilovolts (1000 volts) |
| KW | Kilowatts (1000 watts) |
| KVA | Kilovolt-Ampere |
| KVAR | Kilovolt-Ampere-Reactance |
| PF | Power Factor |
| C | Capacitance (in microfarads) |
| f | Frequency |
| p | PI – 3.1415927 |
| 1mF | 1 x 10-6 farads (MFD) |
$$(KW \hspace{3 pt}= \hspace{3 pt} \frac{V * A * sqrt{3} * PF}{1000})$$
$$(KVA \hspace{3 pt}= \hspace{3 pt} \frac{V * A * sqrt{3}}{1000})$$
$$(KVAR \hspace{3 pt}= \hspace{3 pt} \frac{(2PF)C(KV)^{2}}{1000})$$
$$(C \hspace{3 pt}= \hspace{3 pt} \frac{KVAR * 1000}{(2PF)(KV)^{2}})$$
$$(Line \hspace{3 pt}Amps \hspace{3 pt}= \hspace{3 pt} \frac{KVA * 1000}{sqrt{3} V})$$
$$(Capacitor \hspace{3 pt}Amps \hspace{3 pt}= \hspace{3 pt} \frac{KVAR * 1000}{sqrt{3} V})$$
$$(Capacitor \hspace{3 pt}Amps \hspace{3 pt}= \hspace{3 pt} \frac{(2PF)CV * 10^{-6}}{sqrt{3} V})$$
$$(PF \hspace{3 pt}= \hspace{3 pt} \frac{KW}{KVA})$$
$$(KW \hspace{3 pt}= \hspace{3 pt}KVA * PF)$$
$$(KVA \hspace{3 pt}= \hspace{3 pt}sqrt{KW^{2} + KVAR^{2}})$$

